Prizmės Tūris ir Paviršiaus Plotas: Skaičiavimo Formulės ir Pavyzdžiai

Prizmė yra erdvinis kūnas, sudarytas iš dviejų lygiagrečių pagrindų ir šoninių paviršių, kurie yra stačiakampiai. Šiame straipsnyje aptarsime, kaip apskaičiuoti prizmės tūrį ir paviršiaus plotą, naudingas formules ir praktinius pavyzdžius.

Kas yra prizmė?

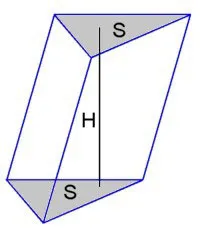
Prizmė – tai geometrinė figūra, kurios pagrindai gali būti bet kokie lygiagretainiai. Šoninės briaunos yra statmenos pagrindui, o prizmės aukštinė žymima H. Yra įvairių prizmės tipų, pavyzdžiui:

• Trikampė prizmė, kurioje pagrindai yra trikampiai.
• Keturkampė prizmė, kurioje pagrindai yra keturkampiai.
• Stačiakampis gretasienis, kurio pagrindai yra stačiakampiai.
• Kubas, kuris yra ypatingas stačiakampio gretasienis, kurio visos briaunos yra lygios.

Prizmės tūrio formulės

Prizmės tūris V gali būti apskaičiuojamas naudojant šią formulę:

V = S_p × h

Čia:

• S_p – pagrindo plotas
• h – prizmės aukštinė

Pagrindo ploto apskaičiavimas

Pagrindo plotas S_p priklauso nuo prizmės tipo. Pavyzdžiui:

• Trikampės prizmės atveju: S_p = (1/4) × n × a² × cot(180°/n), kur n yra kraštinių skaičius.
• Keturkampės prizmės atveju: S_p = a², kur a yra kraštinės ilgis.

Šoninio paviršiaus ploto formulė

Šoninio paviršiaus plotas S_s apskaičiuojamas taip:

S_s = n × a × h

Kur:

• n – kraštinių skaičius
• a – pagrindo kraštinės ilgis
• h – aukštinė

Paviršiaus ploto formulė

Viso paviršiaus plotas S_pav skaičiuojamas pagal šią formulę:

S_pav = S_s + 2 × S_p

Pavyzdžiai

1. Stačiakampio gretasienio tūris

Jei turime stačiakampį gretasienį, kurio ilgis a, plotis b, ir aukštis c:

V = a × b × c

Viso paviršiaus plotas apskaičiuojamas taip:

S_pav = 2 × (a × b + b × c + a × c)

2. Kubas

Kubas, kaip stačiakampis gretasienis, kurio visos sienos yra kvadratai, turi:

V = a³

O viso paviršiaus plotas:

S_pav = 6 × a²

Praktinės prizmės taikymo sritys

Prizmės tūrio ir paviršiaus ploto skaičiavimai naudojami įvairiose srityse, tokiose kaip:

• Statyba – skaičiuojant medžiagų kiekį.
• Moksliniai tyrimai – analizuojant erdvines figūras.
• Inžinerija – projektuojant įvairius objektus.

Susiję skaičiuoklės ir ištekliai

Jei norite išsamiau susipažinti su prizmės tūrio ir paviršiaus ploto skaičiavimais, rekomenduojame pasinaudoti skaičiuoklėmis, kuriose galite lengvai apskaičiuoti įvairių geometrinių figūrų parametrus.

Taip pat, galite pasidomėti apie kūgių tūrio skaičiavimą, kuris susijęs su panašiomis formulėmis, tačiau apima ir apotemos sąvoką, kuri yra šoninė kūgio briauna.

Išvada

Prizmės tūrio ir paviršiaus ploto skaičiavimai yra svarbūs tiek moksliniuose, tiek praktiniuose kontekstuose. Supratimas apie tai, kaip apskaičiuoti šiuos parametrus, padeda geriau suprasti geometrines figūras ir jų taikymą kasdieniame gyvenime.