Trapecijos Ploto Apskaičiavimas: Formulės ir Pavyzdžiai

Trapecija yra keturkampis, turintis du lygius pagrindus, ir jos plotas gali būti apskaičiuojamas naudojant kelias formules. Pagal trapecijos ploto formulę, plotas (S) skaičiuojamas taip:

$$S = frac{(a+b)cdot h}{2}$$

Kur:

• a – pirmas trapecijos pagrindas
• b – antras trapecijos pagrindas
• h – trapecijos aukštinė

Trapecijos Ploto Apskaičiavimas

Apskaičiuoti trapecijos plotą yra paprasta, kai turime visus reikiamus matmenis. Pavyzdžiui, tarkime, kad turime trapeciją, kurios pagrindai yra 8 cm ir 6 cm, o aukštinė yra 5 cm. Naudodami formulę:

$$S = frac{(8 + 6)cdot 5}{2} = frac{14 cdot 5}{2} = 35 , cm^2$$

Taigi, šios trapecijos plotas yra 35 kvadratiniai centimetriai.

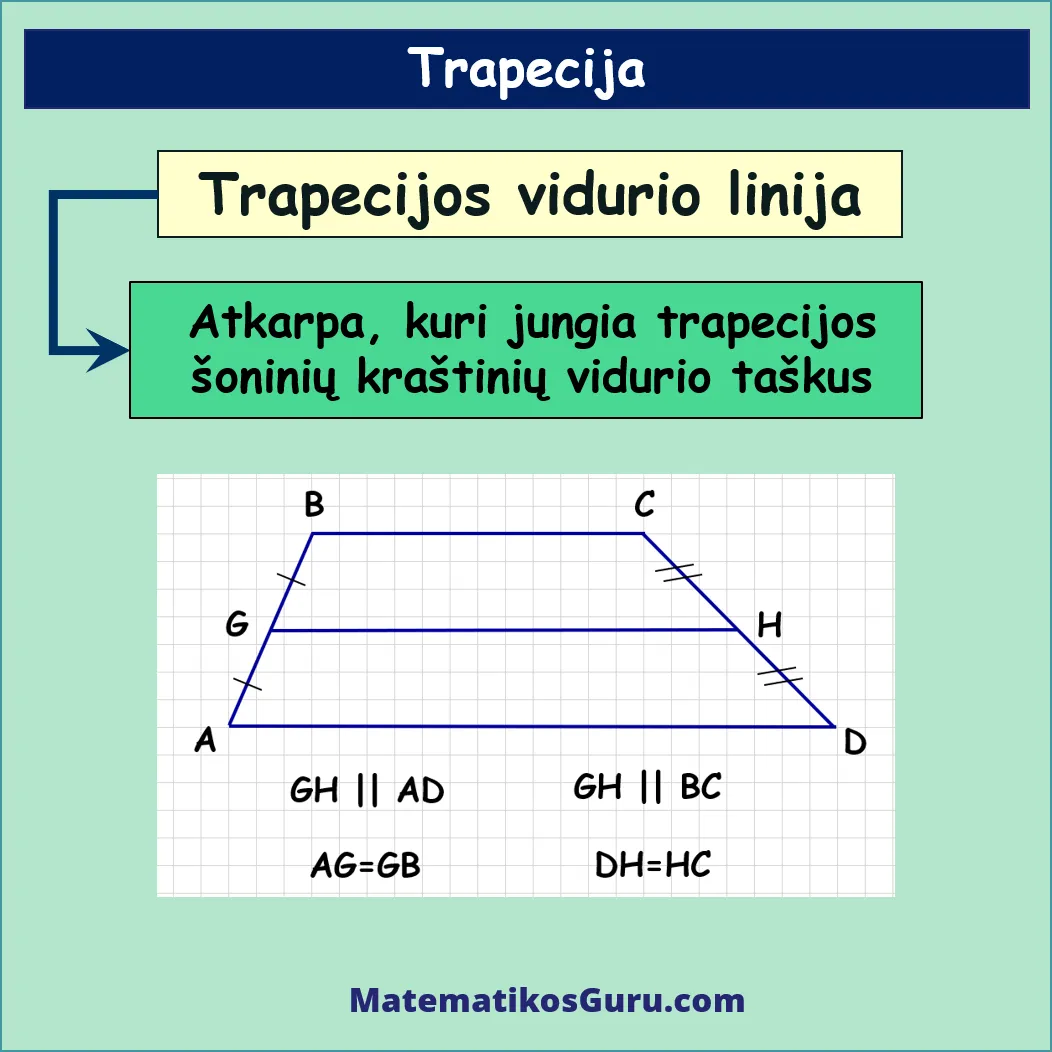
Trapecijos Ploto Formulė Pagal Vidurinę Liniją

Kitas būdas apskaičiuoti trapecijos plotą – tai naudoti vidurinę liniją (m):

$$S = m cdot h$$

Kur:

• m – vidurinė linija
• h – aukštinė

Vidurinė linija yra lygi vidurkiui (a + b)/2, taigi, plotą galima apskaičiuoti ir šiuo būdu.

Praktiniai Pavyzdžiai

Pavyzdys 1

Tarkime, turime trapeciją, kurios pagrindai yra 10 cm ir 4 cm, o aukštinė – 3 cm. Pirmiausia, apskaičiuokime vidurinę liniją:

$$m = frac{10 + 4}{2} = 7 , cm$$

Dabar galime apskaičiuoti trapecijos plotą:

$$S = m cdot h = 7 cdot 3 = 21 , cm^2$$

Pavyzdys 2

Dabar pažiūrėkime į trapeciją su pagrindais 12 cm ir 8 cm bei aukštine 4 cm. Pirmiausia apskaičiuokime plotą su pagrindine formule:

$$S = frac{(12 + 8) cdot 4}{2} = frac{20 cdot 4}{2} = 40 , cm^2$$

Trapecijos Ploto Apskaičiavimo Nauda

Suprasti, kaip apskaičiuoti trapecijos plotą, yra svarbu ne tik matematikos užduotims, bet ir realiame gyvenime. Šios žinios gali būti naudingos architektūroje, statyboje, dizaino projektuose ir netgi kasdieninėse situacijose, tokiose kaip sodo planavimas.

Papildomos Formulės Susijusios Su Ploto Apskaičiavimu

Be trapecijos, yra ir kitų geometrinių figūrų, kurių plotą galima apskaičiuoti naudojant panašias formules. Pavyzdžiui, lygiasonės trapecijos plotas gali būti apskaičiuojamas naudojant šią formulę:

$$S = frac{a cdot b cdot h}{2}$$

Tai leidžia mums greitai ir efektyviai apskaičiuoti figūrų plotus, kai turime atitinkamus matmenis.

Baigiamieji Žodžiai

Žinodami trapecijos ploto formulę, galite lengviau spręsti įvairias užduotis, susijusias su ploto skaičiavimu. Tai taip pat padeda geriau suprasti geometrijos pagrindus ir taikymus.

Daugiau informacijos apie kitų geometrinių figūrų ploto skaičiavimą galite rasti mūsų straipsnyje apie vijeto teoremą.